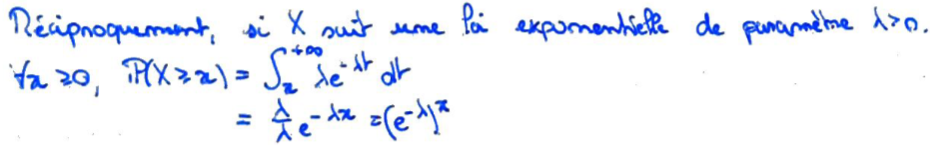Loi exponentielle

Formulaire de report

Problème d'affichage Contenu de la note peu pertinent

Loi exponentielle $\mathcal E(\lambda)$
Modélise certaines durées d'événements aléatoires.
$$f(x)=\lambda e^{-\lambda x}\Bbb 1_{x\in[0,+\infty[}$$

espérance : $E(X)=$ $\frac1\lambda$
variance : $V(X)=$ $\frac1{\lambda^2}$
absence de mémoire

Loi continue, //Loi géométrique

Exercices

Soit $X$ une v.a. À valeur dans ${\Bbb R}$.
On suppose que la loi de $X$ vérifie : $$\forall n,m\in{\Bbb N},\quad {\Bbb P}(X\geqslant n+m\mid X\geqslant n)={\Bbb P}(X\geqslant m)\gt 0.$$
Pour $a\gt 0$, déterminer les lois possibles de $\lfloor aX\rfloor$.

C'est bien une variable aléatoire par mesurabilité de $\lfloor\cdot\rfloor$.

Si $a$ est un entier, la partie entière peut être retirée dans une minoration.

En posant $x=\frac na$ et $y=\frac ma$, on montre que $\lfloor aX\rfloor$ est sans vieillissement.

C'est une variable aléatoire discrète sans vieillissement, c'est donc une Loi géométrique.

Soit $X$ une v.a. À valeur dans ${\Bbb R}$.
On suppose que la loi de $X$ vérifie : $$\forall n,m\in{\Bbb N},\quad {\Bbb P}(X\geqslant n+m\mid X\geqslant n)={\Bbb P}(X\geqslant m)\gt 0.$$
On sait que $a\gt 0$ les lois possibles de $\lfloor aX\rfloor$ sont $\mathcal Geom(1-{\Bbb P}(X\geqslant\frac1a))$.
En déduire les lois possibles pour $X$.

On peut transformer la relation en une relation de puissance.

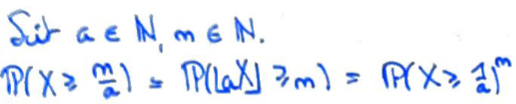
On peut en déduire l'expression de ${\Bbb P}(X\geqslant1)$.

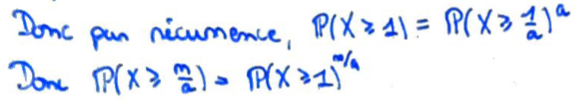
La relation est donc vérifiée pour tout rationnel.

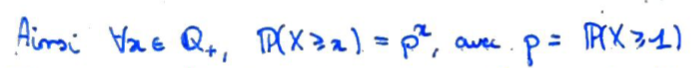
Par continuité à gauche et densité, c'est valable dans ${\Bbb R}^+$ tout entier en $X$ suit une loi exponentielle.

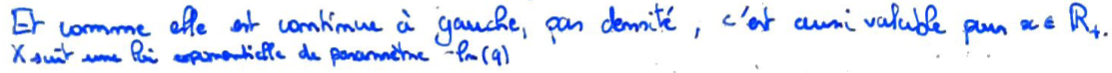
Réciproquement, une loi exponentielle est sans vieillissement.